Method: Condition Number in Numerical Analysis

Condition number of a function measures how much the outputof the function (ie. $y$) can change for a small change in the input (i.e. $x$). The number evaluate the sensitivity of the function when error or change encounted in input.

$$\begin{align*} \Delta x \rightarrow \Delta y ? \end{align*}$$

Function with a low condition number is said to be well-conditioned or ill-conditioned when condition number is high.

Consider the following set-up:

$x = (x_1, \dots, x_m)^T \in R^m, y = (y_1, \dots, y_n)^T \in R^n$
and $y_i = f_i(x_1, \dots, x_m)$\ where $f_i: R^m \rightarrow R \hspace{20pt} i \in [1, n]$

Question: What is the impact of perturbation $\Delta x$ of $x_i$, with respect to $y_i$?

$$\begin{align*} y_i + \Delta y = f_i (x_1 + \Delta x_1, \dots, x_m + \Delta x_m) \hspace{3pt} \text{for} \hspace{3pt} i = 1, \dots, m \end{align*}$$

Example : We are interested in solving the problem

$Ay = b$, $y \in R^n$, $A \in R^{n \times n}$, $b \in R^n$

Assuming $A$ to be regular , we obtain $y = A^{-1} b$

Consider a perturbated problem, we need to address the following problem:

$\begin{align*} y + \Delta y = \underset{\text{truncation error}}{(A + \Delta A)^{-1}}(b + \Delta b) \end{align*}$ where $\Delta A \in R^{n \times n}$, $\Delta b \in R^n$, $\Delta b \in R^n$, $\Delta y \in R^n$

$\begin{equation*} \Delta y_i = \delta_i (x + \Delta x) - \delta_i(x)\\ \Delta y_i = \sum_{i = 1}^m \frac{\partial \delta_i(x)}{\delta x_i}\cdot \Delta x + O (|\Delta x|^2) \end{equation*}$

$\begin{align*} \frac{\Delta y_i}{y_i} = \underset{\text{Condition Number}\kappa_{ij}(x)}{\sum_{i = 1}^m \frac{\partial \delta_i(x)}{\partial x_j} \cdot \frac{x_j}{\delta_i(x)} }\cdot \frac{\delta x_j}{x_j}\\ \end{align*}$

There exists a rule of thumb of conditionn number $\kappa_ij(x)$ : If $\kappa_ij(x) = 10^k$, it indicates you may lose up to $k$ digits of precision

Here gives an simple example of Addition:

$\begin{equation*} y = \delta (x_1, x_2) = x_1 + x_2, x_1, x_2 \in R \setminus \lbrace 0 \rbrace\\ k_1 = \frac{\partial \delta}{\partial x_1}\cdot \frac{x_1}{\delta} = \frac{x_1}{x_1 + x_2} = \frac{1}{1 + \frac{x_2}{x_1}}\\ k_2 = \frac{1}{1+ \frac{x_1}{x_2}} \end{equation*}$

In this example, we have high condition number if $\frac{x_1}{x_2} \sim 1$. In other words, the function is not stable when $\frac{x_1}{x_2} \sim 1$

Apart from that, the following examples also give high condition number:

• Finite Difference: $$ \frac{f(x + h) - f(x)}{h}$$
• Exponential Expansion: $$ e^{-10} = 1 - 10 + \frac{100}{2} - \frac{1000}{6} \cdots $$

The function is ill-conditioned when $x < 0$. To avoid the instability, we can simply change our problem to $\frac{1}{e^x}$ for $x < 1$. The follwing grpah gives a comparision to original problem and modified problem by calculating the relative error: $\sum_{i = 1}^{20} \frac{x^i}{i!}$

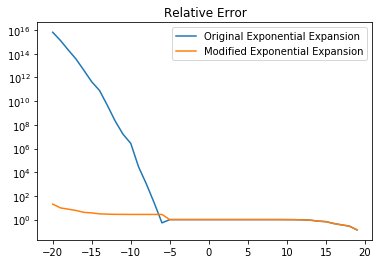
From the above example, we can know that stability is an character in evaluating uncertainty of a model since small perturbation may lead to exponential effect in ill-conditioned model. In the later session, we will learn how to quanifying uncertainty step-by-step.